Il Teorema di Bayes
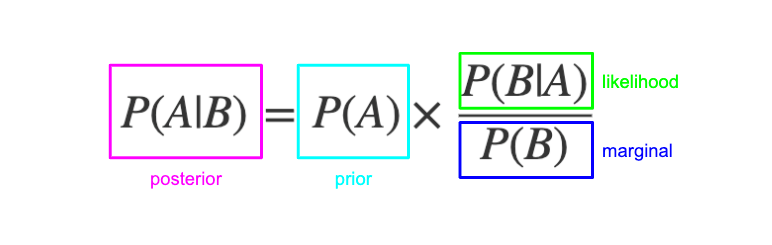
Il Teorema di Bayes è uno strumento fondamentale nella teoria della probabilità che ci permette di aggiornare le nostre credenze sulla base di nuove informazioni. Esso è utilizzato in vari campi, dalla medicina alla finanza all’intelligenza artificiale, per analizzare dati e prendere decisioni più accurate.
Componenti chiave del teorema
Il Teorema di Bayes si basa su tre componenti chiave:
- Probabilità a priori: La probabilità di un evento prima di osservare qualsiasi dato. È la nostra credenza iniziale sull’evento, basata su informazioni precedenti o su una conoscenza generale.
- Probabilità condizionata: La probabilità di un evento dato che un altro evento si è verificato. È la probabilità che l’evento A si verifichi, sapendo che l’evento B si è già verificato.
- Probabilità a posteriori: La probabilità di un evento dopo aver osservato i dati. È la nostra credenza aggiornata sull’evento, basata sulla probabilità a priori e sui dati osservati.
Esempi pratici del Teorema di Bayes
Ecco alcuni esempi di come il Teorema di Bayes viene applicato in situazioni reali:
- Diagnostica medica: Un medico può utilizzare il Teorema di Bayes per valutare la probabilità che un paziente abbia una particolare malattia, dato i suoi sintomi e i risultati dei test.
- Filtraggio dello spam: I filtri antispam utilizzano il Teorema di Bayes per classificare i messaggi di posta elettronica come spam o non spam, in base alla presenza di parole chiave o altri modelli.
- Previsione del tempo: I meteorologi utilizzano il Teorema di Bayes per prevedere la probabilità di pioggia, neve o altri eventi meteorologici, basandosi sui dati storici e sulle condizioni attuali.
Applicazioni del Teorema di Bayes
Il Teorema di Bayes trova applicazioni in una vasta gamma di campi, tra cui:
| Campo | Applicazioni |
|---|---|
| Medicina | Diagnostica, trattamento delle malattie, valutazione dei rischi |
| Finanza | Analisi degli investimenti, gestione del rischio, previsione dei prezzi |
| Intelligenza artificiale | Apprendimento automatico, elaborazione del linguaggio naturale, visione artificiale |
| Scienza dei dati | Analisi dei dati, inferenza statistica, modellazione predittiva |
Applicazioni del Teorema di Bayes nell’Intelligenza Artificiale

Il teorema di Bayes è uno strumento fondamentale nell’intelligenza artificiale (IA), in particolare nell’apprendimento automatico, dove viene utilizzato per modellare la probabilità di eventi futuri basandosi su dati passati. Questo teorema offre un modo sistematico per aggiornare le nostre credenze alla luce di nuove informazioni, permettendo ai sistemi di IA di apprendere e adattarsi in modo efficiente.
Inferenza Probabilistica
Il teorema di Bayes consente di eseguire l’inferenza probabilistica, ovvero il processo di calcolo della probabilità di un evento non osservato, dato un evento osservato. In termini più semplici, possiamo usare il teorema di Bayes per prevedere la probabilità di un evento futuro in base alle informazioni che abbiamo già. Ad esempio, un sistema di IA che analizza le recensioni dei clienti potrebbe utilizzare il teorema di Bayes per prevedere la probabilità che un nuovo prodotto riceva una valutazione positiva, in base alle recensioni dei prodotti precedenti.
Ruolo del Teorema di Bayes nella Classificazione e Previsione
Il teorema di Bayes svolge un ruolo fondamentale nella classificazione e nella previsione di eventi nei sistemi di IA. La classificazione implica l’assegnazione di un elemento a una categoria specifica in base alle sue caratteristiche. Ad esempio, un sistema di IA che classifica le e-mail come spam o non spam utilizzerà il teorema di Bayes per calcolare la probabilità che un’e-mail sia spam in base alle parole che contiene.
Esempi di Algoritmi Basati sul Teorema di Bayes, Bayesian
Diversi algoritmi di apprendimento automatico si basano sul teorema di Bayes. Due esempi notevoli sono i filtri Bayesiani e le reti Bayesiane.
Filtri Bayesiani
I filtri Bayesiani sono algoritmi che utilizzano il teorema di Bayes per filtrare i dati e identificare le informazioni più rilevanti. Questi filtri sono ampiamente utilizzati nell’elaborazione del linguaggio naturale, nella visione artificiale e nell’analisi dei segnali. Un esempio di filtro Bayesiano è il filtro di spam, che utilizza il teorema di Bayes per classificare le e-mail come spam o non spam in base alle parole che contengono.
Reti Bayesiane
Le reti Bayesiane sono modelli grafici che rappresentano le relazioni di dipendenza probabilistica tra variabili. Queste reti utilizzano il teorema di Bayes per calcolare la probabilità di un evento, dato che altri eventi correlati sono noti. Le reti Bayesiane sono utilizzate in una vasta gamma di applicazioni, tra cui la diagnosi medica, la previsione del rischio finanziario e l’analisi di dati genetici.
Inferenza Probabilistica con Diagramma di Rete Bayesiana
Un diagramma di rete Bayesiana è un modo visivo per rappresentare le relazioni di dipendenza tra variabili. In un diagramma di rete Bayesiana, ogni nodo rappresenta una variabile e ogni arco rappresenta una relazione di dipendenza probabilistica tra due variabili.
[immagine di un diagramma di rete Bayesiana]
Nel diagramma sopra, il nodo “A” rappresenta la variabile “Allergia”, il nodo “S” rappresenta la variabile “Sintomi” e il nodo “D” rappresenta la variabile “Diagnosi”. Gli archi indicano che “Allergia” influenza “Sintomi” e “Sintomi” influenza “Diagnosi”.
Utilizzando il teorema di Bayes, possiamo calcolare la probabilità di una diagnosi specifica, dato che un paziente ha determinati sintomi e un’allergia. Ad esempio, possiamo calcolare la probabilità che un paziente abbia una diagnosi di “Asma”, dato che ha sintomi di “Tosse” e un’allergia ai “Pollini”.
Approfondimenti sul Teorema di Bayes: Bayesian

Il Teorema di Bayes, come strumento fondamentale dell’inferenza probabilistica, offre un potente framework per aggiornare le nostre credenze alla luce di nuove informazioni. Tuttavia, come ogni strumento, presenta delle limitazioni e si presta a essere integrato in approcci più avanzati per affrontare situazioni complesse.
Limitazioni del Teorema di Bayes
Il Teorema di Bayes si basa sulla definizione di probabilità a priori, ovvero la probabilità di un evento prima di osservare qualsiasi dato. La precisione di queste probabilità a priori è cruciale per l’accuratezza delle inferenze Bayesiane. In molti casi, ottenere probabilità a priori accurate può essere difficile o impossibile, a causa della mancanza di dati o della complessità del problema.
Ad esempio, se volessimo prevedere la probabilità che un paziente abbia una specifica malattia, dovremmo conoscere la probabilità a priori di quella malattia nella popolazione. Se non disponiamo di dati sufficienti sulla prevalenza della malattia, la nostra probabilità a priori potrebbe essere imprecisa, influenzando negativamente l’accuratezza della nostra inferenza.
Inoltre, il Teorema di Bayes può essere computazionalmente costoso in situazioni con un gran numero di variabili o quando le probabilità a priori sono complesse. La necessità di calcolare probabilità condizionali per ogni possibile combinazione di eventi può diventare un ostacolo computazionale significativo.
Reti Bayesiane Dinamiche
Le reti Bayesiane dinamiche (DBN) estendono il Teorema di Bayes per gestire sistemi che cambiano nel tempo. Le DBN rappresentano le relazioni di dipendenza tra le variabili in un sistema dinamico, consentendo di modellare l’evoluzione temporale delle probabilità.
Le DBN sono utilizzate in diverse applicazioni, come la previsione del tempo, l’analisi finanziaria e il monitoraggio dei sistemi medici. Ad esempio, in un sistema di monitoraggio medico, una DBN potrebbe essere utilizzata per prevedere la probabilità di un paziente di sviluppare una complicanza, tenendo conto dei suoi parametri vitali e della sua storia medica.
Apprendimento Bayesiano
L’apprendimento Bayesiano è un approccio all’apprendimento automatico che utilizza il Teorema di Bayes per aggiornare le probabilità a priori alla luce di nuovi dati. Invece di definire manualmente le probabilità a priori, l’apprendimento Bayesiano le stima dai dati stessi.
Un esempio di apprendimento Bayesiano è la classificazione Bayesiana Naïve. Questo algoritmo assume che le variabili siano indipendenti tra loro, semplificando il calcolo delle probabilità condizionali. La classificazione Bayesiana Naïve è utilizzata in diverse applicazioni, come il filtraggio dello spam e la classificazione dei testi.
Applicazioni del Teorema di Bayes con Dati Incompleti o Incerti
Il Teorema di Bayes può essere applicato in situazioni con dati incompleti o incerti, utilizzando tecniche di inferenza probabilistica. Queste tecniche consentono di stimare le probabilità mancanti o di gestire l’incertezza nei dati.
Ad esempio, in un sistema di raccomandazione, il Teorema di Bayes potrebbe essere utilizzato per stimare la probabilità che un utente sia interessato a un prodotto, anche se non ha mai interagito con esso in precedenza. Il sistema potrebbe utilizzare informazioni come le preferenze dell’utente, le recensioni dei prodotti e le interazioni di altri utenti simili per stimare la probabilità di interesse.
Confronto con Altri Approcci
Il Teorema di Bayes è un potente strumento per l’inferenza probabilistica, ma non è l’unico approccio disponibile. Altri metodi, come le reti neurali, offrono approcci alternativi per modellare e prevedere i dati.
Le reti neurali sono sistemi di apprendimento automatico ispirati al cervello umano, che possono apprendere relazioni complesse tra i dati. Mentre il Teorema di Bayes si basa su probabilità esplicite, le reti neurali apprendono modelli di dati attraverso l’ottimizzazione di parametri.
La scelta del metodo più appropriato dipende dal problema specifico e dalle risorse disponibili. Il Teorema di Bayes è particolarmente utile quando si dispone di un modello probabilistico chiaro e di dati a priori accurati. Le reti neurali, d’altra parte, sono più flessibili e possono apprendere modelli complessi, ma richiedono grandi quantità di dati per essere addestrate.
Ever wondered how your favorite streaming service recommends movies you might enjoy? It’s all thanks to the magic of Bayesian reasoning! This powerful approach to probability, bayesian , helps algorithms understand your preferences and predict what you’ll like next.
So, next time you’re scrolling through recommendations, remember the Bayesian brain behind the scenes, working tirelessly to make your viewing experience more enjoyable.
Bayesian statistics, like a detective piecing together clues, uses prior knowledge to refine predictions. Speaking of clues, you might be interested in learning more about the success story of mike lynch wife – a couple that clearly has a knack for making things work! Just like Bayesian analysis helps us make better decisions, understanding the dynamics of successful relationships can provide valuable insights into human behavior.
